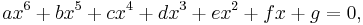Sextic equation

In mathematics, a sextic equation is a polynomial equation of degree six. It is of the form:

ax^6%2Bbx^5%2Bcx^4%2Bdx^3%2Bex^2%2Bfx%2Bg=0,\,

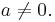
where a \neq 0.

The coefficients a, b, c, d, e, f, g are members of a field, (typically the rational numbers, the real numbers or the complex numbers), and 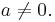a \neq 0.

Because they have an even degree, normal sextic functions appear similar to normal quartic functions when graphed, except they may possess an additional local maximum and local minimum each. The derivative of a sextic function is a quintic function.

Since a sextic function is a polynomial with even degree, it has the same limit when the argument goes to positive or negative infinity. If a is positive, then the function increases to positive infinity at both sides; and thus the function has a global minimum. Likewise, if a is negative, it decreases to negative infinity and has a global maximum.

Another name for a sextic equation is a hexic equation.

Solvable sextics

Some sixth degree equations can be solved by factorizing into radicals, but other sextics cannot. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise to the field of Galois theory.[1]

It follows from Galois theory that a sextic equation is solvable in term of radicals if and only if its Galois group is contained either in the group of order 48 which permutes the roots as the isometries of a regular octahedron permute its vertices or in the group of order 72 which stabilizes a partition of the set of the roots into two subsets of three roots.

There are formulas to test either case, and, if the equation is solvable, compute the roots in term of radicals.[2]

The general sextic equation can be solved in terms of Kampé de Fériet functions.[1] A more restricted class of sextics can be solved in terms of generalised hypergeometric functions in one variable using Felix Klein's approach to solving the quintic equation.[1]

See also

References

  1. ^ a b c Mathworld - Sextic Equation
  2. ^ T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757
By name
By degree
0  · 1  · 2  · 3  · 4  · 5  · 6  · 7